TLDR. Hyperelliptic curves are really cool and doubly so because they can potentially generate groups of unknown order. But how do they work, and how do we determine how secure they are?
Introduction
In a recent IACR ePrint note 1, Samuel Dobson and Steven Galbraith proposed the use of the Jacobian group of a hyperelliptic curve of genus 3 as a candidate group of unknown order. The authors conjecture that at the same level of security, Jacobian groups of genus 3 hyperelliptic curves outperform the ideal or form class group in terms of both operational speed and representation size. Given the recent explosion of applications of groups of unknown order — verifiable delay functions, accumulators, trustless SNARKs, just to name a few — it is no wonder that this proposal was met with much enthusiasm. This note summarizes the mathematics involved in the hope to enable rapid deployment, but perhaps also to argue the case for caution.
For an engineer to deploy any group in practice, he must know:
- How to select public parameters for a target security level.
- How to represent group elements on a computer, and how to sample non-trivial group elements.
- How to apply the group law to pairs of group elements and, optionally, how to compute inverses.
This post summarizes the theory of hyperelliptic curves from an engineering point of view; that is to say, with an eye to answering these questions.
Divisors
Let $ \mathbb{F} $ be a field and $\mathbb{F}[x,y]$ the ring of polynomials in two variables. A curve is the set of points satisfying $0 = C(x,y) \in \mathbb{F}[x,y]$, along with the designated point $\infty$ called the point at infinity. While the coefficients of $C$ must belong to $\mathbb{F}$, when we consider the points satisfying the curve equation, we include points drawn from any extension field of $\mathbb{F}$. Let $\mathbf{C}$ denote this set of points. Such a curve is singular when for some point $P$, $C(P) = \frac{\partial{}C}{\partial{}x} (P) = \frac{\partial{}C}{\partial{} y} (P) = 0.$ (Just use the same old analytical rules for computing partial differentials; there is a finite field analogue for the definition of differentials that does not rely on infinitesimal quantities.) We need a non-singular curve $C$.
Let $\mathbb{E}$ be some finite extension of $\mathbb{F}$. The coordinate ring of $C$ over $\mathbb{E}$ is the quotient ring $K_C(\mathbb{E}) = \frac{\mathbb{E}[x,y]}{\langle C \rangle}$. The elements of this ring are polynomials in $x$ and $y$, but two such polynomials are considered equivalent if they differ by a multiple of $C$. Equivalently, $K_C(\mathbb{E})$ is the space of functions $\mathbb{E}^2 \rightarrow \mathbb{E}$ where we ignore the values the functions take in points not on the curve (so $\{P | C(P)=0\} \rightarrow \mathbb{E}$ would be a more precise signature). Furthermore, the function field $L_C$ is the fraction field of the coordinate ring of $C$, or phrased differently, $L_C(\mathbb{E})$ is the field whose elements are fractions with numerator and denominator both in $K_C(\mathbb{E})$.
Let $f(x,y)$ be a function in the coordinate ring $K_C(\mathbb{E})$. The order of vanishing of $f$ at a point $P$, denoted $\mathsf{ord}_f(P)$, is zero if $f(P) \neq 0$, and otherwise the greatest possible $r$ such that $f(x,y) = u(x,y)^r g(x,y)$ for some $g(x,y)$ with $g(P) \neq 0$ and for some uniformizer $u(x,y)$. The univariate analogue is when a polynomial $f(x)$ has a root of multiplicity $r$ at $P$, because in this case $f(x) = (x-P)^r g(x)$ for some $g(x)$ with $g(P) \neq 0$. Let $h(x,y)$ be a rational function from the function field of $L_C(\mathbb{E})$ of $C$, meaning that $h(x,y) = \frac{f(x,y)}{g(x,y)}$ for some $f(x,y), g(x,y) \in K_C(\mathbb{E})$. Then define the order of vanishing of $h$ in $P$ to be $\mathsf{ord}_h(P) = \mathsf{ord}_f(P) – \mathsf{ord}_g(P)$. When $f(P) = 0$, we refer to $P$ as a zero, and when $g(P) = 0$ it is a pole.
A divisor of $C$ is a formal sum of points, which is to say, we use the summation symbol but use the resulting expression as a standalone object without ever computing any additions. This formal sum assigns an integer weight to every point on the curve, and has a finite number of nonzero weights. Therefore, any divisor $D$ can be expressed as
$$ D = \sum_{P \in \mathbf{C}} c_P [P] \enspace ,$$ where all weights $c_P \in \mathbb{Z}$, and where the notation $[P]$ serves to identify the point $P$ and to indicate that it is not actually added to any other points.
Given two or more divisors, it is straightforward to compute their sum — just compute the pointwise sum of weights. This means that the set of divisors of $C$, denoted $\mathsf{Div}_C(\mathbb{E})$, is actually a group. Furthermore, define the degree of a divisor to be $\mathsf{deg}(D) = \sum_{P \in \mathbf{C}} c_P$. Then the set of divisors of degree zero is a subgroup: $\mathsf{Div}^0_C(\mathbb{E}) < \mathsf{Div}_C(\mathbb{E})$.
A principal divisor is a divisor $D$ that is determined by a rational function $h(x,y) = \frac{f(x,y)}{g(x,y)} \in L_C(\bar{\mathbb{F}})$, where $\bar{\mathbb{F}}$ is the field closure of $\mathbb{F}$, via
$$ D = \mathsf{div}(h) = \sum_{P \in \mathbf{C}} \mathsf{ord}_h(P) [P] \enspace .$$ Principal divisors always have degree zero. (This fact is rather counterintuitive. It is important to take the sum over all points in the field closure satisfying the curve equation, as well as the point at infinity.) Moreover, the set of principal divisors is denoted by $P_C(\bar{\mathbb{F}})$. It is a subgroup of $\mathsf{Div}_C^0(\bar{\mathbb{F}})$ and the restriction $P_C(\mathbb{E}) = P_C(\bar{\mathbb{F}}) \cap \mathsf{Div}_C^0(\mathbb{E})$ is a subgroup of $\mathsf{Div}_C^0(\mathbb{E})$.
We now have the tools to define the group we will be working with. The group of $\mathbb{E}$-rational points of the Jacobian of $C$ is $J_C(\mathbb{E}) = \frac{\mathsf{Div}_C^0(\mathbb{E})}{P_C(\mathbb{E})}$. Specifically, its elements are equivalence classes of divisors, with two members of the same class being considered equivalent if their difference is principal, or symbolically:
$$D_1 \sim D_2 \quad \Leftrightarrow$$
$$\exists f(x,y), g(x,y) \in K_C(\mathbb{E}) \, : \, D_1-D_2 = \sum_{P \in \mathbf{C}} (\mathsf{ord}_f(P) – \mathsf{ord}_g(P)) [P] \enspace .$$
Addition in this group corresponds to addition of divisors. However, there is no obvious way to choose the smallest (in terms of representation size) element from the resulting equivalence class when representing divisors as dictionaries mapping points to integers. For this we need to switch to a computationally useful representation of group elements.
Mumford Representation
The previous definitions hold for any generic curve $C$. Now we restrict attention to curves of the form $C(x,y) = f(x) – y^2$, where $f(x,y) \in \mathbb{F}[x]$ has degree $2g + 1$ and where $\mathbb{F}$ is a large prime field. This corresponds to a hyperelliptic curve and the number $g$ is referred to as the curve’s genus.
A divisor $D$ is called reduced if it satisfies all the following conditions:
- It is of the form $\sum_{P \in \mathbf{C} \backslash \{ \infty \}} c_P([P] – [\infty])$.
- All $c_P >= 0$.
- Let $P = (x,y)$, then $y = 0$ implies $c_P \in \{0,1\}$.
- Let $P = (x,y)$ and $\bar{P} = (x,-y)$ and $y \neq 0$, then either $c_P = 0$ or $c_{\bar{P}} = 0$ (or both).
- $\sum_{P \in \mathbf{C} \backslash \{ \infty \}} c_P \leq g$.
There is exactly one reduced divisor in every equivalence class in $J_C$, and every reduced divisor corresponds to exactly one equivalence class in $J_C$. Therefore, we could have defined the Jacobian of $C$ to be the set of reduced divisors, except that the group law does not correspond with addition of divisors any more: the sum of two reduced divisors is not reduced. One could start from the addition rule for divisors and follow that up with a reduction procedure derived from the curve equation and the definition of principal divisors. However, it is by no means clear how this reduction procedure would work.
Mumford came up with a representation of reduced divisors that is conducive to finding the reduced representative of a divisor equivalence class. This representation consists of two polynomials, $U(x), V(x)$, such that all the following are satisfied.
- $U(x)$ is monic.
- $U(x)$ divides $f(x) – V(x)^2$.
- $\mathsf{deg}(V(x)) < deg(U(x)) \leq g$.
The polynomial $U(x)$ is simply the polynomial whose roots are the $x$-coordinates of all finite points in the reduced divisor: $U(x) = \prod_{i=0}^{d-1}(x-x_i)$. The polynomial $V(x)$ interpolates between all finite points on the reduced divisor. It takes the value (or rather: one of two possible options) of the curve at all $x_i$. The divisor associated with $(U(x), V(x))$ is therefore $D = \sum_{i=0}^{d-1}([(x_i, V(x_i))] – [\infty])$. To find the Mumford representation of a divisor whose finite points are given by $\{P_i = (x_i, y_i)\}_{i=0}^{d-1}$, simply set $U(x)$ to the product as above, and determine $V(x)$ via Lagrange interpolation: $V(x) = \sum_{i=0}^{d-1}y_i \prod_{j \neq i} \frac{x-x_j}{x_i-x_j}$.
The cool thing about representing divisors as polynomials is their suitability for plots. Of course, to draw an elliptic or hyperelliptic curve we need to pretend that the field over which they are considered is continuous. However, many of the geometric intuitions drawn from continuous plots carry over to the discrete case.
Consider the elliptic curve $y^2 = x^3 -x + 1$, plotted below. Also plotted are the sets of intersection points of the lines $U(x) = 0$ and $y – V(x) = 0$ (dashed lines) for the following group elements presented here in Mumford representation:
- $A: U(x) = x+1.2$ and $V(x) = 0.678$
- $B: U(x) = x$ and $V(x) = 1$
- $C: U(x) = x-1.27$ and $V(x) = -1.33$.
All these intersections do lie on the curve and therefore these polynomial pairs do represent valid group elements. The fact that $U(x)$ is linear and $V(x)$ is constant corresponds to the curve having genus 1, and also to the collapse of the set into just one intersection point for each group element. So we can use $A$, $B$, and $C$ simultaneously to denote the group element, as well as its representative as a point on the curve.
Let’s compute the group operation. The reduced divisor of the group element $A$ is $[A] – [\infty]$ and that of $B$ is $[B] – [\infty]$. Their divisor sum is $[A]+[B]-2[\infty]$. In order to find the reduced divisor from the same equivalence class, we must find a principal divisor that upon addition with this sum sends the two finite points to just one and decrements by one the weight of the point at infinity. Phrased differently, we must find a rational function $h(x,y) = f(x,y) / g(x,y)$ such that $[A] + [B] -2[\infty] + div(h) = [A+B] – [\infty]$, for some curve point which we denote with abusive additive notation as $A+B$.
The plot below shows one such option, plotting $f(x,y)$ in blue and $g(x,y)$ in red. Since $f$ and $g$ are themselves rational functions, their divisors must have degree zero. Indeed, $f$ has a pole of order 2 in $\infty$, and $g$ has a pole of order 3 there. Note that the finite intersection point between the red and blue lines does not appear in this formal sum of points: this absence corresponds with $g(x,y)$ and $1/f(x,y)$ having equal and opposite orders of vanishing in this point. The same phenomenon occurs at infinity, where $1/f(x,y)$ subtracts three from that point’s weight and $g(x,y)$ adds two back.
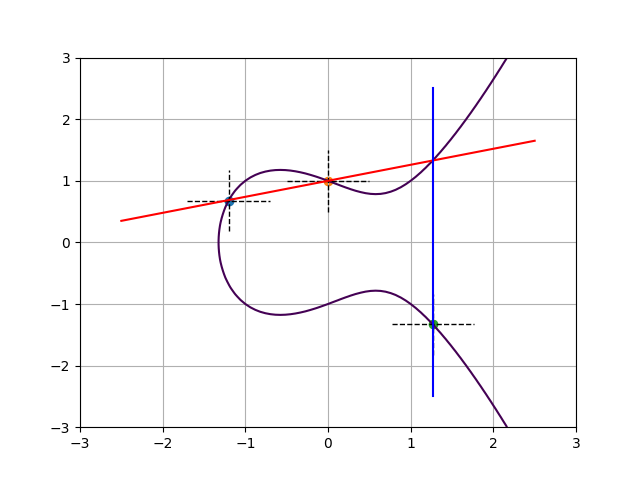
In other words, the chord-and-tangent rule for elliptic curves is just a special case of the Jacobian group law!
Let’s move on to a more complicated example. Below we have a plot of the genus 2 hyperelliptic curve $y^2 = x^5 -2x^4 -7x^3 +8x^2 + 12x$, with group elements $A$, $B$, and $C$ given by Mumford polynomials (dashed lines)
- $A: U(x) = (x+1.96)(x+1.5)$ and $V(x) = 7.926x + 14.320$
- $B: U(x) = (x-3.05)(x-5.03)$ and $V(x) = 19.204x – 60.383$
- $C: U(x) = (x-1.467)(x-0.263)$ and $V(x) = 4.230x – 3.003$.
For each of these group elements, the lines $U(x) = 0$ and $V(x) = y$ intersect the curve in two points. In fact, this is a property of genus 2 curves, meaning that one can represent any group element by its two intersection points.
Since every group element corresponds to two elements on the curve, we have $\mathsf{div}(A) = [A_1] + [A_2] – 2[\infty]$, for the two points that represent $A$; and similarly for $\mathsf{div}(B)$ and $\mathsf{div}(C)$. To compute the group operation, we start from $\mathsf{div}(A) + \mathsf{div}(B) = [A_1] + [A_2] + [B_1] + [B_2] – 4[\infty]$ and search for a principal divisor $\mathsf{div}(h)$ such that sends the four finite points to two. One could start by finding the lowest degree univariate interpolating polynomial between the four points; this gives $f(x,y)$ which is plotted below in red. Note that $f(x,y)=0$ intersects the curve in six points $(A_1, A_2, B_1, B_2, \bar{C_1}, \bar{C_2})$, of which five are depicted in the plot. Furthermore, $f(x,y)$ has a pole of order 6 at infinity. Likewise, $g(x,y)$ intersects the curve in four points $(C1, C2, \bar{C1}, \bar{C2})$ and has a pole of order 4 at infinity. Therefore, the divisor equation
$$\mathsf{div}(A) + \mathsf{div}(B) – \mathsf{div}(C)$$
$$= [A1]+[A2]+[B1]+[B2]-4[\infty]-[C1]-[C2]+2[\infty]$$
$$= [A1]+[A2]+[B1]+[B2]+[\bar{C1}]+[\bar{C2}]-6[\infty]$$
$$-([C1]+[\bar{C1}]+[C2]+[\bar{C2}]-4[\infty])$$
$$=\mathsf{div}(f) – \mathsf{div}(g)$$ shows that as divisors, $A+B$ and $C$ are indeed apart by a principal divisor.
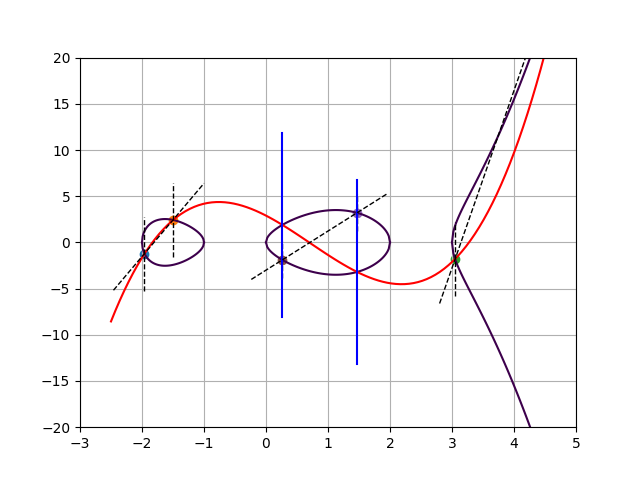
The two plots shown so far suggest a shortcut for representing group elements and computing the group operation thereon. Simply:
- Represent group elements as points or sets of points on the curve.
- When adding two group elements, fit a polynomial through all points and find the new points where it intersects the curve.
- Flip the $y$-coordinates of these new points; this set is the new group element.
A natural question to ask is whether this intuition extends to curves of higher genus. That might be the case for all I know, but my intuition says “no”. Indeed, for curves of genus $\geq$ 3 no explicit point addition formulae are known and the preferred modus operandi for representing elements and operating on them is via their Mumford representations.
So how do we perform the group operation on Mumford pairs? That’s exactly what Cantor’s algorithm does. (Due to David Cantor and not Georg.)
Cantor’s Algorithm
Computes the composition of elements in the Jacobian group of the curve $y^2 = f(x)$.
- Input: $(U1, V1), (U2, V2) \in (\mathbb{F}[x])^2$
- Output: $(U, V) \in (\mathbb{F}[x])^2$
- Use the extended Euclidean algorithm to find the Bezout coefficients $h_1, h_2, h_3 \in \mathbb{F}[x]$ and $d \in \mathbb{F}[x]$ such that $d = \mathsf{gcd}(U_1, U_2, V_1 + V_2) = U_1h_1 + U_2h_2 + (V_1+V_2)h_3$.
- $V_0 \leftarrow (U_1V_2h_1 + U_2V_1h_2 + (V_1V_2 + f)h_3) / d$
- $U \leftarrow U_1U_2 / d^2$ and $V \leftarrow V_0 \, \mathsf{mod} \, U$
- $U’ \leftarrow (f-V^2)/U$ and $V’ \leftarrow -V \, \mathsf{mod} \, U’$
- $(U, V) \leftarrow (U’ / \mathsf{lc}(U’), V’)$
- If $\mathsf{deg}(U) > g$ go back to step 4
- Return $(U,V)$
The intuition behind the algorithm is that the polynomial $V_0$ is constructed to represent the divisor $\mathsf{div}(A) + \mathsf{div}(B)$. This polynomial is then reduced using the curve equation such that the degree decreases but the equivalence class remains the same. After reduction, the output is another Mumford pair.
Note that the polynomials considered all have coefficients drawn from $\mathbb{F}$, the plain old base field. This corresponds to restricting the Jacobian group to only elements defined over $\mathbb{F}$. Formally, let $\phi$ be the Frobenius map sending points $(x,y)$ to $(x^p,y^p)$ and $\infty$ to $\infty$, where $p$ is the order of the field $\mathbb{F}$. Then $\phi$ sends a divisor $D = \sum_{P \in \mathbf{C}} c_P [P]$ to $\phi(D) = \sum_{P \in \mathbf{C}} c_P [\phi(P)]$. A Jacobian group element (i.e., an equivalence class of divisors) is defined over $\mathbb{F}$ iff $\phi(D)-D$ is a principal divisor. In fact, by selecting the polynomials from the ring of polynomials over the base field, we guarantee that the Mumford pair determines a particular reduced divisor — the representative of its equivalence class — that remains unchanged under $\phi$. This implies that we can straightforwardly sample a non-trivial group element simply by sampling a Mumford representative; it is guaranteed to represent an element that is defined over $\mathbb{F}$.
Finally, the inverse of a group element $(U, V)$ is $(U, -V)$ and the identity is (1, 0).
Hyperelliptic Jacobians as Groups of Unknown Order
In the case of hyperelliptic Jacobians, the public parameters boil down to the curve equation and really, to the right hand side of $y^2 = f(x)$. Dobson and Galbraith recommend using an hyperelliptic curve of genus $g=3$, such that $f(x)$ has degree $2g+1=7$. Without loss of generality, $f(x)$ can be chosen to be monic, so there are only 7 coefficients left to determine. These should be drawn uniformly at random but such that $f(x)$ is irreducible.
The group is to be defined over a large enough prime field. In this case, an adaptation of Hasse’s theorem due to André Weil bounds the order of the group as
$$ (\sqrt{p}-1)^{2g} \leq #J_C(\mathbb{F}) \leq (\sqrt{p}+1)^{2g} \enspace .$$
Obviously we can’t determine the cardinality exactly because the whole point is that it should be unknown! However, the order must be sufficiently large because otherwise the discrete logarithm problem wouldn’t be hard.
The cheapest way to determine the order of the group is to determine the number points over $\mathbb{F}$ on the curve. For elliptic curves this can be accomplished using Schoof’s algorithm. There is an adaptation of this algorithm for genus 2 with complexity $O((\mathsf{log} \, p)^7)$. Dobson and Galbraith are unclear about what happens for genus 3, but another recent ePrint note 2 refers to work by Abelard for point counting in genus 3 curves that runs in $\tilde{O}((\mathsf{log} \, p)^{14})$ time.
Hyperelliptic curves of high genus admit index calculus attacks that are subexponential. For low genus $g \geq 3$, there is an attack in expected time $\tilde{O}(p^{2-2/g})$, which outperforms generic square root algorithms, whose complexity is $O(p^{g/2})$. For genus 2 curves the generic square root algorithms are faster.
There is a reduction due to Smith for translating the discrete logarithm problem on a genus 3 hyperelliptic curve to an elliptic one that works a sizable proportion of the time. After that translation, there is an algorithm due to Diem with estimated running time $O(p (\mathsf{log} \, p)^2)$.
The complexity of these attacks are plotted as a function of the number of bits of $p$ in the next figure.
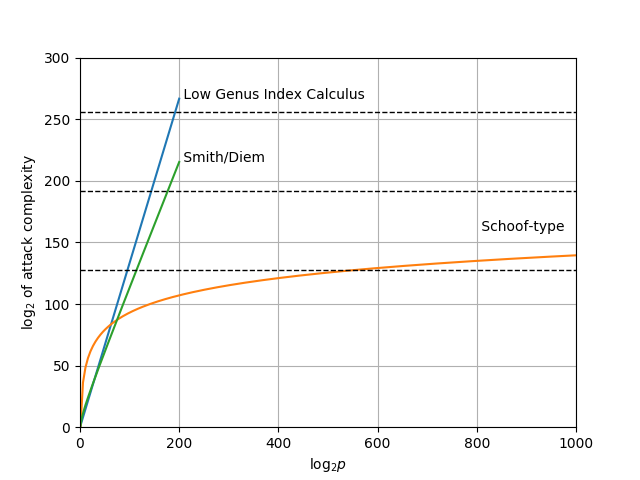
The orange line, which plots the complexity of the Schoof-type algorithm, is alarming. While it does cross the dotted line indicating 128 bit security (at $\mathsf{log}_2 \, p = 540$) it only crosses the 192 and 256 bit security lines for impractically large field sizes. The point of targeting 192 or 256 bits of security is not to hedge against improvements in the attacker’s computing power, because $2^{128}$ elementary operations is impossible within the lifetime of the universe according to our current understanding of its physical laws. Rather, the point of targeting $192$ or $256$ bits of security is to hedge against algorithmic improvements that cause the attack to require less computing work than anticipated. With respect to this objective, even a relatively minor improvement to the point counting algorithm would break the hedge as it decreases the actual security of conservative parameter choices by a large margin and massively increases the size of the base field required to provide the same target security level. In other words, it is not possible to err on the side of paranoia. Anyone looking to deploy genus 3 hyperelliptic curves for groups of unknown order must therefore be absolutely confident in their understanding of the best possible attack.
The exact complexity of point counting in curves of genus 3 remains a major open question with, until now, little practical relevance. However, as an alternative to understanding the complexity of point counting more exactly, it may be possible to generate groups of unknown order from similar mathematics but such that point counting does have the requisite complexity. For instance, we should not discount higher genera than 3, nor more generic abelian varieties.
Lastly, Dobson and Galbraith note that it is often easy to sample elements of small but known order. The capability to sample elements of known order violates the adaptive root assumption. The proposed solution is to instead use to the group $[s!] J_C(\mathbb{F}) = \{s! \, \mathbf{e} \, | \, \mathbf{e} \in J_C(\mathbb{F})\}$ for some large enough integer $s$ determined in the public parameters. This restriction kills off all elements of order up to $s$. When relying on the adaptive root assumption, for instance because Wesolowski’s proof of correct exponentiation is being used, it pays to represent the element $s! \, \mathbf{e}$ as $\mathbf{e}$, so that the verifier can verify that $s! \, \mathbf{e}$ is indeed a multiple of $s$ simply by performing the multiplication. Dobson and Galbraith argue that choosing $s = 60$ should guarantee a reasonable level of security, with $s = 70$ being the option of choice for paranoiacs.
To be honest, I am not sure I understand the argument by which the recommendation $s = 60$ is derived. It is something along the following lines. In Schoof’s algorithm (and derivatives) for point counting, an important step is to find points of order $\ell$. This translates to determining the order of the group modulo $\ell$, and via the Chinese Remainder Theorem the order of the group as an integer without modular reduction. Therefore, when we assume that determining the order of the group is hard, then there must be an $s$ such that constructing points of order $\ell > s$ is hard. The time complexity of this step of Schoof’s algorithm is $\tilde{O}(\ell^6 \mathsf{log} \, p)$ whereas the memory complexity is only $\tilde{O}(\ell^4 \mathsf{log}\, p)$, meaning that for large $\ell$, the running time will be the limiting factor. Extrapolating from implementation results reported on by Abelard in his thesis, setting $s = 60$ should be well beyond the capacity of an adversary running in a reasonable amount of time.
Personally, I prefer to draw the $\tilde{O}(\ell^6 \mathsf{log} \, p)$ complexity curve and set parameters depending on where it intersects with the target security level. The graph plotted below assumes $p \approx 2^{540}$ and pretends as though the polylogarithmic factor hidden by the $\tilde{O}$ notation is one. Note that the horizontal axis is the value of $\ell$ itself, and not its logarithm. For good measure I include the memory complexity (dashed orange line), in addition to the computational complexity (full blue).
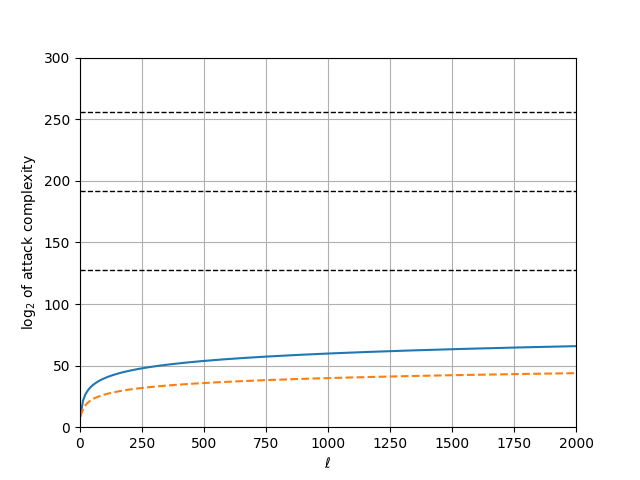
Based on this graph, I disagree with Dobson and Galbraith and recommend against using the Jacobian of a hyperelliptic curve for applications where the adaptive root assumption is supposed to be hard — unless with a solution that is different from restricting the group to $[s!] J_C(\mathbb{F})$.
Conclusion
Algebraic geometry, which is the field of mathematics that studies elliptic and hyperelliptic curves, is a powerful and versatile tool for generating cryptographic primitives. The recent proposal for generating groups of unknown order from hyperelliptic curves of genus 3, while exciting, is not without concerns. Specifically, a variant of Schoof’s point counting algorithm determines the group’s order in polynomial time, albeit a large degree polynomial. This complexity makes the selection of parameters to err on the side of safety nearly impossible and as a result, an accurate understanding of the best performing algorithm for this task is of paramount importance to anyone looking to deploy these groups in practice. Furthermore, the are algorithms that compute group elements with small but known order, violating the adaptive root assumption. These groups should not be used in constructions that require this assumption to hold, even if computing the order of the whole group is hard.
Nevertheless, the caution argued for in this article derives from a rather simplistic algorithm for determining the appropriate parameters: plot the computational complexity of the attack as a function of those parameters, and determine where that curve crosses the $2^{128}$ threshold. In reality, the attacker may require other resources as well — for instance, time, memory, parallel CPUs, or communication bandwidth between those CPUs. A more refined analysis may conclude that an assumed bound on the availability of these secondary resources will prohibit an attack long before it reaches $2^{128}$ elementary computational steps. Dobson and Galbraith are certainly not ignorant of the attacks on hyperelliptic curves nor of the standard simplistic methodology for deriving appropriate parameters. Therefore, I expect them to provide a more refined analysis in support of their proposal, perhaps based on other resource constraints. I will read that elaboration with much excitement when it appears.
Further Reading
- Samuel Dobson and Steven Galbraith: “Trustless Groups of Unknown Order with Hyperelliptic Curves” [IACR ePrint]
- Jonathan Lee: “The security of Groups of Unknown Order based on Jacobians of Hyperelliptic Curves” [IACR ePrint]
- Alfred J. Menezes and Ji-Hong Wu and Robert J. Zuccherato: “An elementary introduction to hyperelliptic curves” [link]
- Jasper Scholten and Frederik Vercauteren: “An Introduction to Elliptic and Hyperelliptic Curve Cryptography and the NTRU Cryptosystem” [link]
- Lawrence C. Washington: “Elliptic Curves: Number Theory and Cryptography, second edition” [home page]
- A straightforward implementation in Sage of hyperelliptic curves over prime fields [github repository]