On Noisy Nonlinear Key Agreement
Published on 2018-10-28
On Nonlinear Noisy Key Agreement
TL;DR. A large number of post-quantum key encapsulation mechanisms (KEMs) and public key encryption schemes (PKEs) rely on noisy linear algebra problems. Interestingly, the addition of noise to make otherwise easy problems hard, is a strategy that remains restricted to linear algebra and fails to extend to nonlinear operations. This article explores why.
Noisy key agreement
Key agreement is a protocol by which Alice and Bob each send one message to the other and end up agreeing on a shared secret key. The eavesdropper Eve, who observes all messages in transit (but can’t modify them) remains incapable of computing this secret. The first such protocol was introduced by Diffie and Hellman and bears their names, but the general principle extends to generic algebras and not just commutative group theory.
For instance, let Alice and Bob agree on a common random integer $G$ from a finite ring $R$, such as e.g. the set of $n \times n$ matrices of integers modulo some prime $p$. Moreover, let Alice and Bob each sample their secret, $a$ and $b$ respectively, from this structure as well. They then exchange $\hat{a} = aG$ and $\hat{b} = Gb$, allowing both to agree on the shared key $k = a\hat{b} = \hat{a}b = aGb$. Note that while the order of multiplication is important for matrices, by agreeing beforehand whose secret will be multiplied on which side of G, Alice and Bob circumvent this complication entirely.
 |
|---|
| Fig. 1: Noise-free key agreement (insecure). |
Unfortunately, this protocol is completely insecure. Eve, who sees Alice and Bob agree on G before sending $\hat{a} = aG$ and $\hat{b} = Gb$, can compute $G^{-1}$ and recover both Alice’s and Bob’s secrets, not to mention the shared secret key. Even if the ring disallows efficient computation of an element’s inverse, it remains extremely likely that there is a way to find the solution $b$ to the system of linear equations $Gb = \hat{b}$ and symmetrically for $a$.
The solution that makes the protocol a noisy key agreement protocol is to transmit only an approximation of $aG$ and $Gb$. To see why this makes Eve’s task hard, observe how the error term $\epsilon_b = \hat{b} - Gb$ explodes: $G^{-1}\hat{b} = G^{-1}(Gb + \epsilon_b) = G^{-1}Gb + G^{-1}\epsilon_b = b + G^{-1}\epsilon_b$. Since $G$ is a matrix with uniformly random coefficients, so is $G^{-1}$ and multiplying that by another matrix $\epsilon_b$ — even if it has small coefficients — yields another random ring element that hides $b$ much like a one-time pad.
However, the addition of small noise makes it difficult for Alice and Bob to agree on the same secret. Observe that Alice computes $k_a = a(Gb + \epsilon_b)$ whereas Bob computes $k_b = (aG + \epsilon_a)b$. The trick is implied by the symbols’ case: instead of sampling uniformly random $a$ and $b$, Alice and Bob sample $a$ and $b$ with small coefficients. If $a$, $b$, $\epsilon_a$, and $\epsilon_b$ have small enough coefficients, then Alice’s view $k_a = aGb + a\epsilon_b$ is approximately the same as Bob’s view $k_b = aGb + \epsilon_a b$. As long as the difference $a \epsilon_b – \epsilon_a b$ is small enough, they can proceed to agree on an exact key with one additional message which either reconciles the two views or uses them in combination with error-correcting codes to transmit a wholly new message. In this last case, I like to refer the views $k_a$ and $k_b$ as shared noisy one-time pads or “snow-tipis”.
 |
|---|
| Fig. 2: Noisy key agreement. |
So how small should the secret elements $a$, $b$, $\epsilon_a$, $\epsilon_b$ be? On the one hand, the secrets should not be too small because that reduces Eve’s search space. On the other hand, the secrets cannot be too large because then the difference $a \epsilon_b – \epsilon_a b$ is too large to enable either the reconciliation or transmission strategy. The situation is best described visually. While the unknown bits of the secrets do spread and multiply — and obscure Eve’s view — they also leave some bits of $aGb$ intact; these bits can then be used as secret key material.
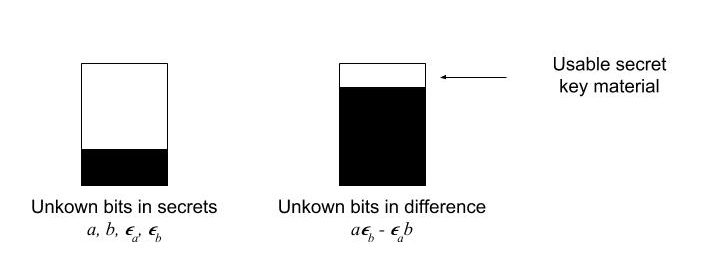 |
|---|
| Fig. 3: Key agreement with usable secret key material. |
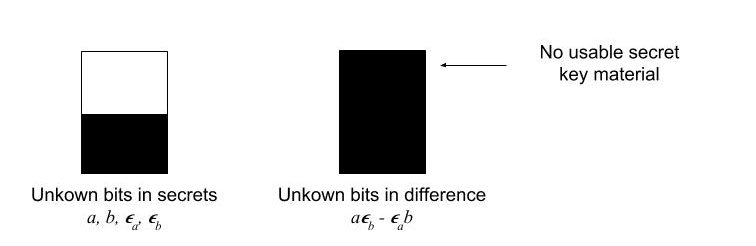 |
|---|
| Fig. 4: Key agreement with no usable secret key material. |
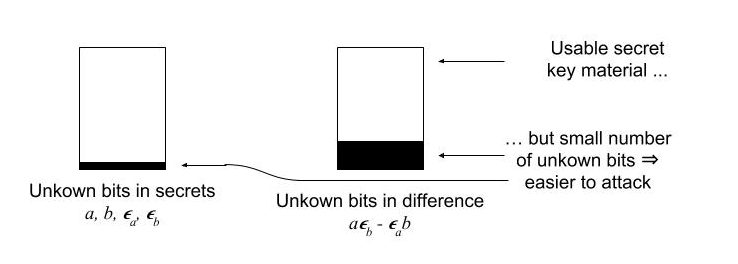 |
|---|
| Fig. 5: Key agreement with attackable secrets. |
Incidentally, Ramstake, my own submission to the NIST PQC Project, does not quite follow this “intact bits” strategy of establishing common secret key material. Instead of having a few unknown bits at fixed locations, the secrets now have a few flipped bits at unknown locations. As long as the difference $a \epsilon_b – \epsilon_a b$ is not too dense, an error correcting code can help extract or transmit secret key material. Interpreting a darker shade of grey as representing a denser error distribution, this gives rise to the following analogous diagram.
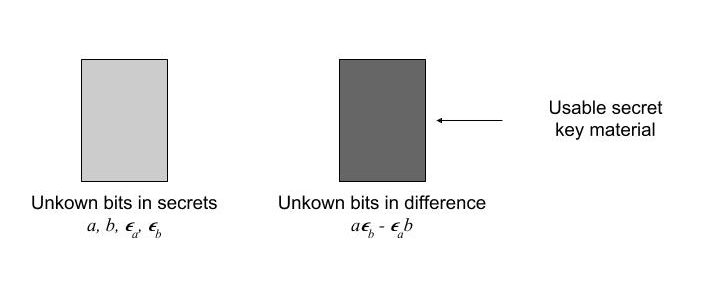 |
|---|
| Fig. 5: Key agreement with noise at unknown locations. |
Nonlinear Noisy Key Agreement
So why are there no nonlinear noisy key agreement protocols, or cryptosystems based thereon? Actually, that premise is not true. There is a submission to the NIST PQC project by the name of CFPKM whose underlying hard problem is polynomial system solving with noise (“PoSSoWN”). Alice and Bob compute their protocol contributions by evaluating a quadratic function $f$, which has small coefficients, in their secret vectors $s_a$ and $s_b$, also with small coefficients, and by adding another small noise term. The underlying protocol is shown in the next figure. Unfortunately, despite the security proof, the cryptosystem was broken within weeks of the submissions’ publication.
The cryptanalysis exploits the observation that the keys computed by Alice and Bob differ only by the difference of element-wise products $f(s_a) \odot e_2 - f(s_b) \odot e_1$, which affects only the lower bits; whereas the high bits of both views are used for the session key. Importantly, these high bits are the same in $b_1 b_2$, which is a value the passive adversary can compute as well.
So why is there no successful cryptosystem based on noisy nonlinear key agreement? The first observation is that the term nonlinear is really only relative to what the function’s arguments are. For instance, the expression $x_1^2 + 2x_1x_2 - x_2^2$ is nonlinear as a function of $(x_1, x_2)$ but linear as a function of $(x_1^2, x_1x_2, x_2^2, x_1, x_2, 1)$. By extending as we did here the vector of arguments of a function to a vector of all monomials occurring in that expression, any expression can be regarded as a linear function. In particular, both Alice’s and Bob’s computation of their proper views of the noisy secret key may be considered as linear transforms on some extended vector of monomials. This observation suggests a two-step approach to the diagrams above that indicate the source of secret key material: the second step captures the familiar linear noisy key agreement. The first step captures the extension of the original arguments into a vector of monomials.
This diagram highlights the origin of the problem: in order for there to be usable secret key material left at the end, the unknown bits in the extended vector of monomials must not be too many. In order for those unknown bits to not be too many, the unknown bits in the original arguments must be even fewer. However, this very salient feature makes these original arguments a vulnerable target for attack.
Conclusion
Why are there so few cryptosystems based on nonlinear noisy key agreement? My answer is twofold:
- Because any such protocol implies a linear noisy key agreement protocol.
- Adding nonlinearity to a linear noisy key agreement protocol makes it less secure.
| comments |
|---|
| December 5, 2018 at 4:52 pm; Davidw: |
| Not sure I understand the “the expression (2 unknowns) is linear as a function of (6 items)” |
| Can you expand on that? Great post otherwise |
| December 5, 2018 at 5:05 pm; Alan Szepieniec: |
| The expression $x_1^2 + 2x_1x_2 - x_2$, or any expression really, is linear if it can be written as matrix $\times$ vector, for some matrix. The question is, what does that vector look like? |
| For instance, $x_1^2 + 2x_1x_2 - x_2$ is not linear if the vector is $v = (x_1, x_2)$ because no matrix $M$ can make $Mv$ equal to this expression. However, the same expression is linear if the vector is $v = (x_1^2, x_1x_2, x_2^2, x_1, x_2, 1)$ because such an $M$ does exist in this case. I’m ignoring here the vertical stacking of column vectors for formatting reasons, but you get the point. |